堆的概念:
n个元素序列 { k1, k2, k3, k4, k5, k6 …. kn } 当且仅当满足以下关系时才会被称为堆:
ki <= k2i,ki <= k2i+1 或者 ki >= k2i,ki >= k2i+1 (i = 1,2,3,4 .. n/2)
如果数组的下表是从0开始,那么需要满足
ki <= k2i+1,ki <= k2i+2 或者 ki >= k2i+1,ki >= k2i+2 (i = 0,1,2,3 .. n/2)
比如 { 1,3,5,10,15,9 } 这个序列就满足 [1 <= 3; 1 <= 5], [3 <= 10; 3 <= 15], [5 <= 9] 这3个条件,这个序列就是一个堆。
所以堆其实是一个序列(数组),如果这个序列满足上述条件,那么就把这个序列看成堆。
堆的实现通常是通过构造二叉堆,因为二叉堆应用很普遍,当不加限定时,堆通常指的就是二叉堆。
二叉堆的概念:
二叉堆是一种特殊的堆,是一棵完全二叉树或者是近似完全二叉树,同时二叉堆还满足堆的特性:父节点的键值总是保持固定的序关系于任何一个子节点的键值,且每个节点的左子树和右子树都是一个二叉堆。
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。
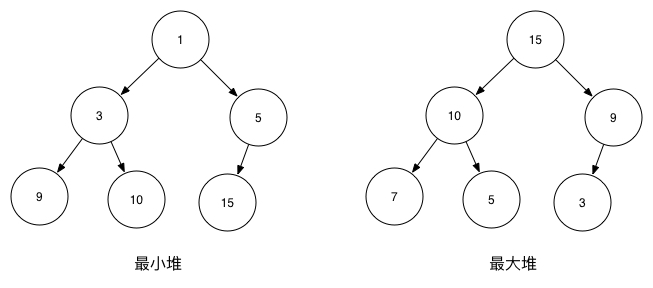
上图中的最小堆对应的序列是: [1,3,5,9,10,15] 满足最小堆的特性(父节点的键值小于或等于任何一个子节点的键值,并且也满足堆的性质 [1 <= 3; 1 <= 5], [3 <= 9; 3 <= 10], [5 <= 15])
上图中的最大堆对应的序列是: [15,10,9,7,5,3] 满足最大堆的特性(父节点的键值大于或等于任何一个子节点的键值,并且也满足堆的性质 [15 >= 10; 15 >= 9], [10 >= 7; 10 >= 5], [9 >= 3])
堆的操作
堆排序
堆排序指的是对堆这种数据结构进行排序的一种算法。其基本思想如下,以最大堆为例:
- 将数组序列构建成最大堆[ A1, A2, A3 .. An],这个堆是一个刚初始化无序区,同时有序区为空
- 堆顶元素A1与最后一个元素An进行交换,得到新的有序区[An],无序区变成[A1 … An-1]
- 交换之后可能导致[A1 … An-1]这个无序区不是一个最大堆,[A1 … An-1]无序区重新调整成最大堆。重复步骤2,A1与An-1进行交换,得到新的有序区[An,An-1],无序区变成[A1 … An-2].. 不断重复,直到有序区的个数为n-1才结束排序过程
构造堆的过程如下(以最大堆为例):
从最后一个非叶子节点开始调整,遍历节点和2个子节点,选择键值最大的节点的键值代替父节点的键值,如果进行了调整,调整之后的两个子节点可能不符合堆特性,递归调整。一直直到调整完根节点。
以序列[3,5,15,9,10,1]为例进行的堆排序:
首先第1步先把数组转换成完全二叉树:
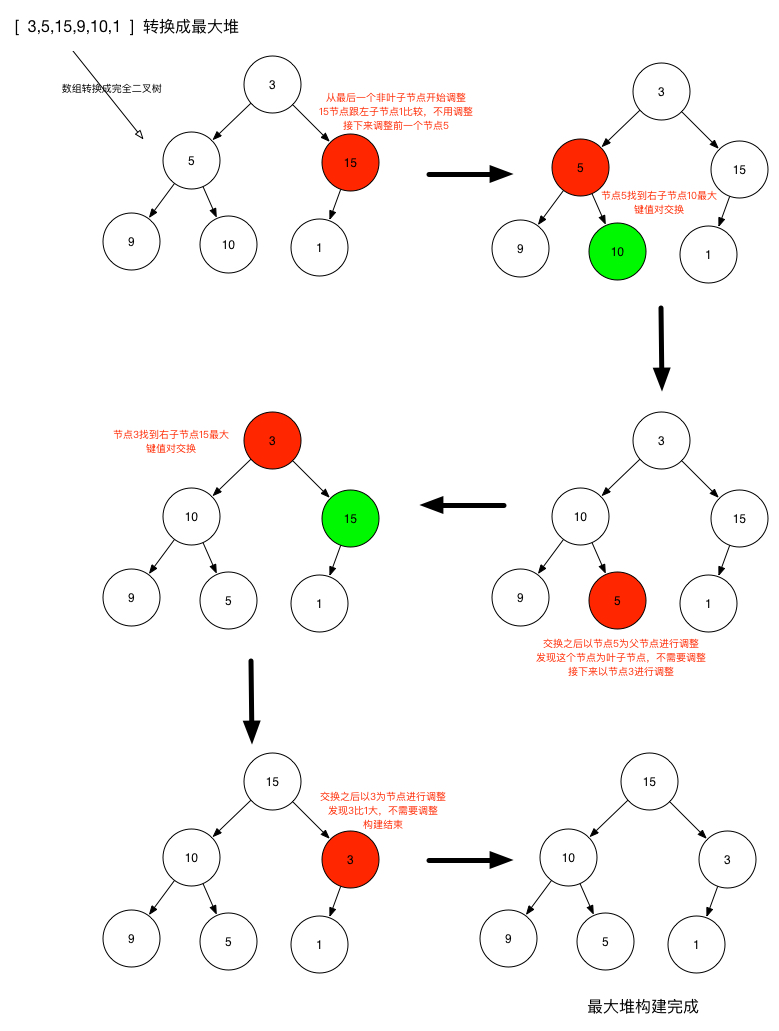
接下来是第2、3步构造有序区和无序区:
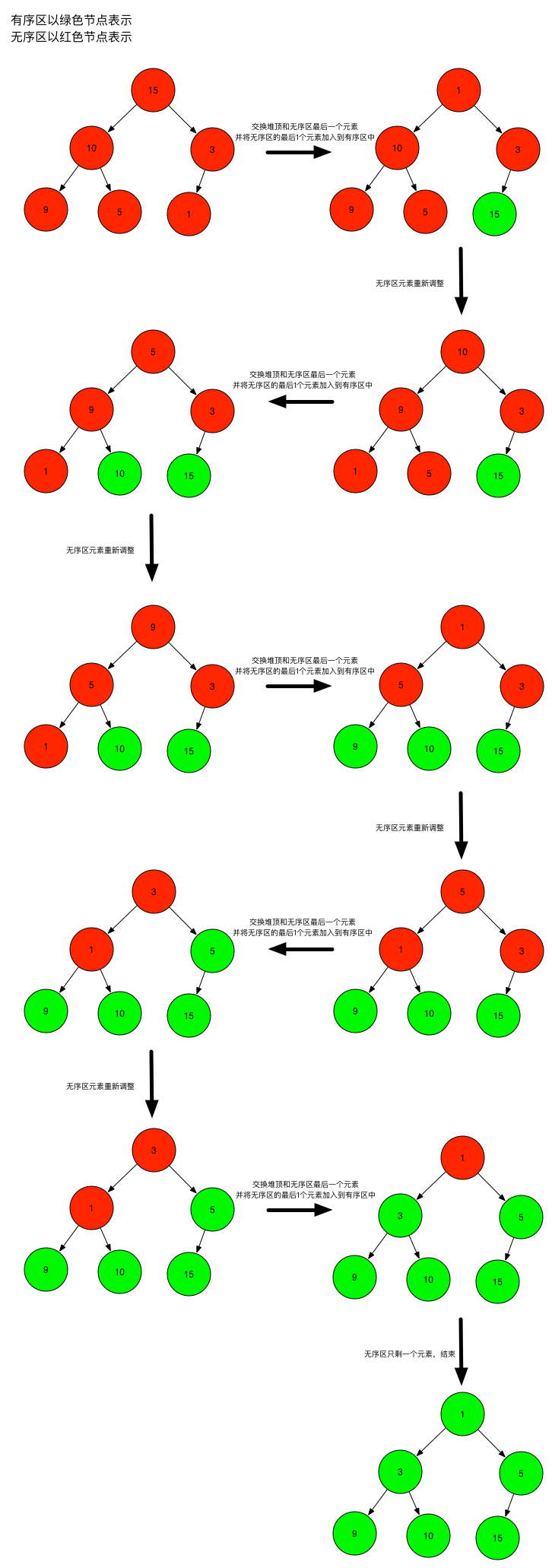
构造完之后有序区的元素依次是:1,3,5,9,10,15
简单地使用java写一下堆排序:
public class HeapSort {
public static void maxHeapify(int[] arr, int size, int index) {
int leftSonIndex = 2 * index + 1;
int rightSonIndex = 2 * index + 2;
int temp = index;
if(index <= size / 2) {
if(leftSonIndex < size && arr[temp] < arr[leftSonIndex]) {
temp = leftSonIndex;
}
if(rightSonIndex < size && arr[temp] < arr[rightSonIndex]) {
temp = rightSonIndex;
}
// 左右子节点的值存在比父节点的值更大
if(temp != index) {
swap(arr, index, temp); // 交换值
maxHeapify(arr, size, temp); // 递归调整
}
}
}
public static void heapSort(int[] arr, int size) {
// 构造成最大堆
buildMaxHeap(arr, arr.length);
for(int i = size - 1; i > 0; i --) {
// 先交换堆顶元素和无序区最后一个元素
swap(arr, 0, i);
// 重新调整无序区
buildMaxHeap(arr, i - 1);
}
}
public static void buildMaxHeap(int[] arr, int size) {
for(int i = size / 2; i >= 0; i --) { // 最后一个非叶子节点开始调整
maxHeapify(arr, size, i);
}
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] arr = { 3, 5, 15, 9, 10, 1};
System.out.println("before build: " + Arrays.toString(arr)); // before build: [3, 5, 15, 9, 10, 1]
buildMaxHeap(arr, arr.length);
System.out.println("after build: " + Arrays.toString(arr)); // after build: [15, 10, 3, 9, 5, 1]
heapSort(arr, arr.length);
System.out.println("after sort: " + Arrays.toString(arr)); // after sort: [1, 3, 5, 9, 10, 15]
}
}
添加
在最大堆[ 15,10,9,7,5,3 ]上添加一个新的元素 11 ,执行的步骤如下:
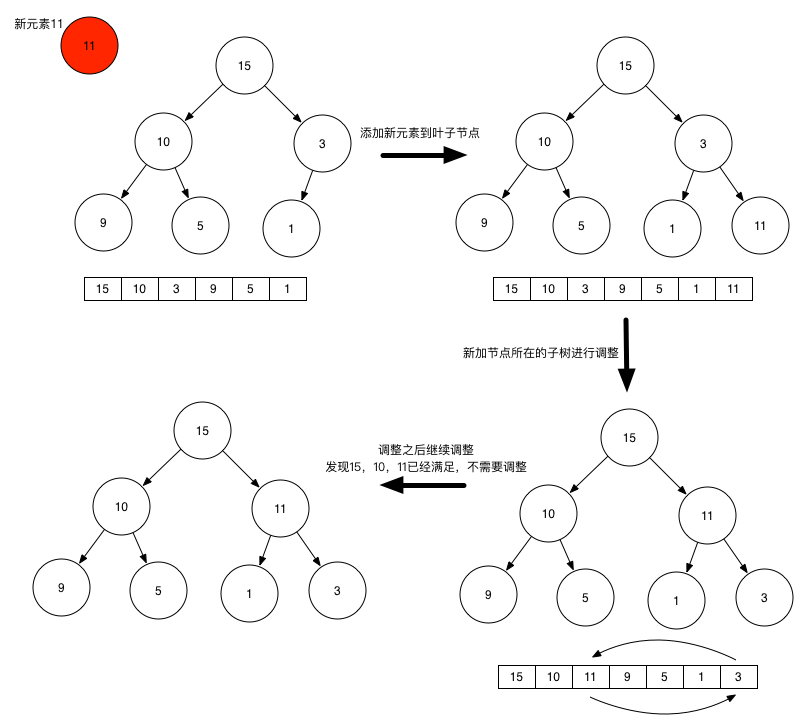
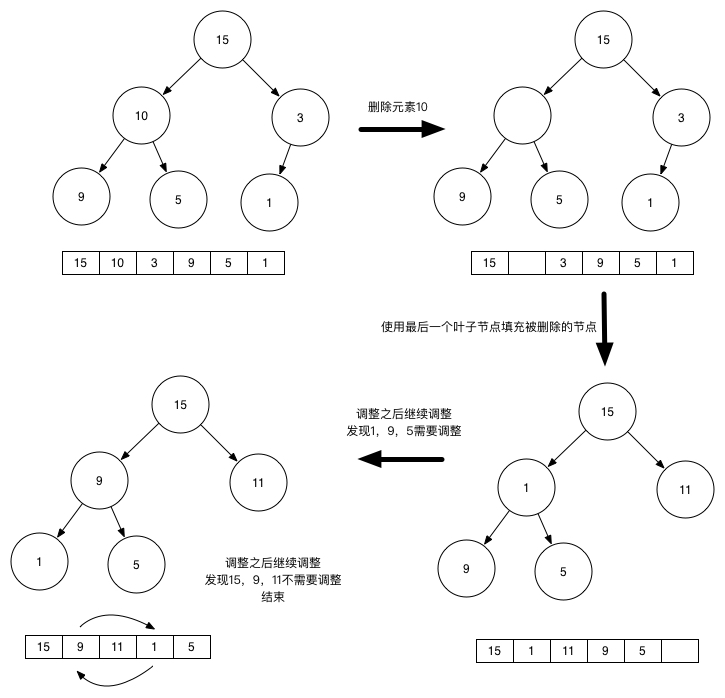
删除
在最大堆[ 15,10,9,7,5,3 ]上删除元素 10 ,执行的步骤如下: